Poutama Parents

WOULDN'T LIFE BE PERFECT 

IF HELPING YOUR CHILD 

WITH THEIR 

HOMEWORK 

WAS THIS EASY?!

BUT IN REALITY, THIS IS WHAT CAN SOMETIMES HAPPEN!

Do you look at the maths homework and think...?!

PARENTS - Below is some information on the NZ math curriculum guidelines and how to help your child at home.

The skills a student requires at each year level are informed by the NZ curriculum, The National Standards and Numeracy Project Material.  The Numeracy Framework is broken up into a series of progressive stages ranging from 0-8.  Each of these stages consists of Knowledge and Strategy skills.  Each stage equates with a curriculum level as outlined below.

Curriculum Level 1	Curriculum Level 2	Curriculum Level 3	Curriculum Level 4	Curriculum Level 5
At the end of two years at school	Year 3& 4	Years 5&6	Years 7&8	Year 9&10
Stage 0 - 4	Stage 5	Stage 6	Stage 7	Stage 8

  

Each stage requires different skills and these are built upon progressively.  Each stage has a different set of knowledge and strategy domains which will be explained later.  Students can be working at different stages for different domains.

Number Knowledge

Each stage has important aspects of knowledge that a student should know in order that they have a secure number base to apply to their solving of problems (strategies) Number knowledge is split into the following domains:

• Number Identification
• Number Sequence and Order
• Grouping/Place Value
• Basic Facts
• Written Recording (to be addressed later on)

Strategy

At different stages children display different thinking.  As they progress through the Number Framework they develop their understanding of strategies that they could use to solve particular problems.  Students then select appropriate strategies that they can use successfully and accurately to solve problems.  The Framework is split into 3 domains, Addition and Subtraction, Multiplication and Division, Proportions and Ratios.  There are 8 strategies though the first three are often grouped together and are generally completed during the first year of schooling.  The NZMaths website describes the strategy stages as:

• Stage 0-3: Counting from One - children can solve problems by counting from one, either using materials or in their head.
• Stage 4: Advanced Counting - children can solve problems by counting in ones, or by skip counting, starting from numbers other than one.
• Stage 5: Early Additive - children can solve simple problems by splitting up and adding together the numbers in their head.
• Stage 6: Advanced Additive - children use a range of different methods to solve more challenging problems in their head.
• Stage 7: Advanced Multiplicative - children use a range of different methods to solve multiplication and division problems in their head.
• Stage 8: Advanced Proportional - children can solve complicated problems involving fractions, decimals and percentages using a combination of methods.

Strategy Methods

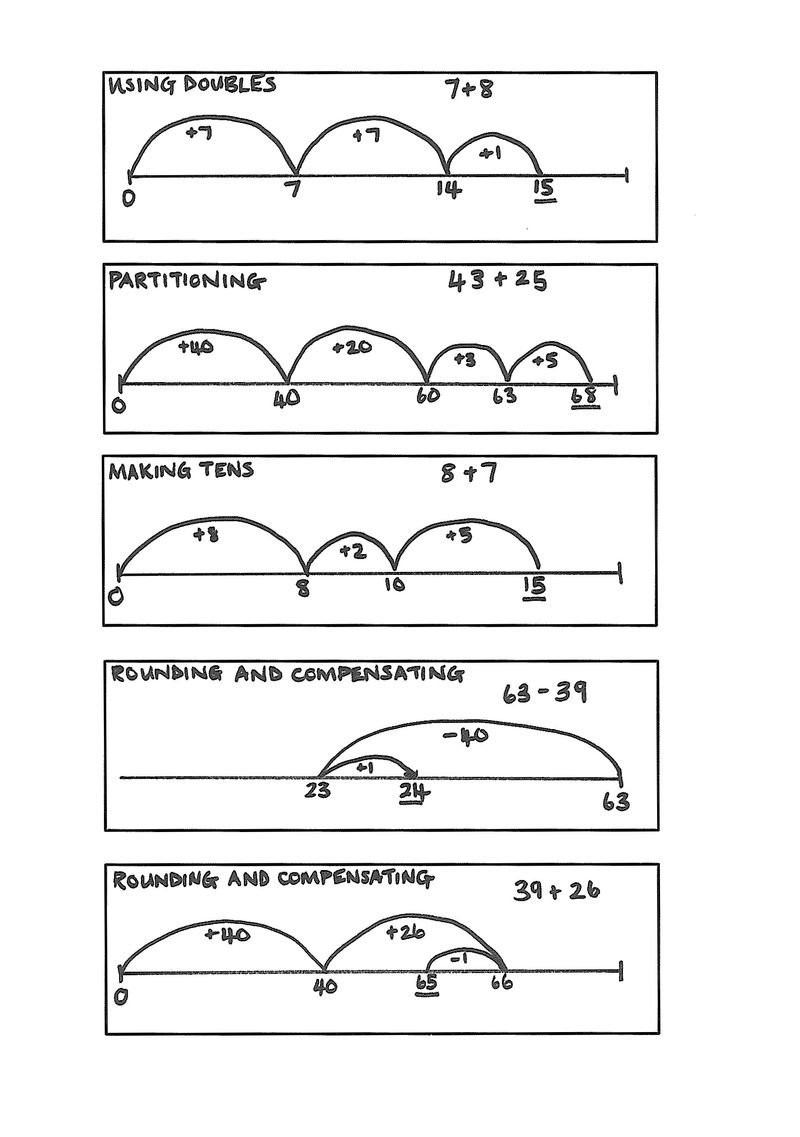
From Stage 5 upwards students are exposed to different methods of solving problems. Drawing on the knowledge facts they have learned is key.  Students will select their preferred strategies from the strategies they are exposed to. Some of the methods they are shown are as follows:

	ADDITION AND SUBTRACTION
Strategy	Explanation
Doubles	8 + 7 =  8 + 8 – 1=
Making Tens	8 + 7 = (7 can be split into a 5 and 2) 8 + 2 = 10 10 + 5 = 15	84 – 8 (8 can be split into 4 and 4) 80 – 4 – 4 =
Partitioning	43 + 25 = (40 + 20) + (3+5) =	76 – 22= (70 – 20) – (6 – 2) =
Rounding and Compensating	39 + 26 = 40 + 26 - 1=	63 – 39 = 63 – 40 +1 =
Reversibility	39 + 24 = 63	so    63 – 39 = 24

These strategies are taught throughout the stages and are used with fractions and decimals in later stages. 

	MULTIPLICATION AND DIVISION
Strategy	Explanation
Repeated Addition/Subtraction	4 x 6 as (6+6) + (6+6) = 12+12 = 24	24  6 = 24 24 – (6 + 6 + 6 +6) =
Doubling and Halving	4 x 6 = 2 x12
Rounding and Compensating	9 x 6 = (10 x 6) - 6
Partitioning	24 x 6 = (20 x 6) + (4 x 6) OR 43 x 12 = (40 x 10) + (3 x 10) +                 (40 x 2) + (3 x 2)
Reversibility	63  7 = 9    so  9 x 7 = 63

For Proportions and Ratios work students draw on multiplication and division strategies as outlined above.  Below are links to more posters that demonstrate some of the strategies your child may use.

                             

  

The successful use of these strategies also relies on the student have the required knowledge at a particular stage. Some of these strategies are also stepping stones in the lead up to knowledge items at a higher stage.

It is probably best not to try and teach these strategies to your child, however, they can be used to support your child's learning.  They provide an insight into how your child will be thinking and give you an idea of the process they will have gone through.  They may be useful for your understanding when your child tries to explain what they have been learning at school or they are experiencing some difficulties.

Models to Support Learning

There are many models and diagrams we can use to support learning.  It is important to note though that standard written methods (algorithms) for solving calculations are not introduced until Stage 6.  A couple of examples that can be used across all stages are shown here.

The empty number line is a useful and can aid in teaching a multitude of strategies at different levels.

The multiplication grid is another useful model, particularly with problems involving two or more digits or decimals.

How Can You Help Your Child at Home? 

Click on the picture below to be taken to a video explaining how you can support your child's learning at home.

The Numeracy Home-School Partnership document also provides useful information about supporting children's mat

hematical understandings and some of the challenges they may face.

COUNTING

There are two initial skills: Say the counting words in order – 1, 2, 3, 4, 5… Match the counting sequence to the objects one by one. The next significant idea, when those skills have been mastered is: the last number name used gives the number of objects.

Challenges for children:

Counting in order is challenging because there is no pattern or repetition in the first twelve numbers. Other challenges: Counting backwards, for example, 14, 13, 12, 11, 10, 9, 8… and naming the number before and the number after a particular number. Learning “teen” numbers: 11, 12, 13, 14, 15, 16, 17, 18, 19. Learning to count over the decade, for example, 18, 19, 20, 21, 22 and 38, 39, 40, 41, 42. Progressing past counting only what they can see (they may wrongly think a thousands block is 600 because that is all they see).

Ways to develop their understanding:

Practising counting forwards and backwards by 1s, 2s, 5s, and 10s using everyday items around them, for example, vegetables, fruit, steps, sheep, cows, table cutlery, hands, and pegs. Counting in 10s from 10 and also from single-digit numbers, for example, 4, 14, 24… and backwards …24, 14, 4.

PLACE VALUE

Place value involves grouping in 10s. There are only 10 digits (0–9). The same digits are used in different positions for different values. Zero is an important “place holder”. There are patterns in the way numbers are formed, for example, 20–29, 30–39. When counting from 0 to 20, there are some cultural differences. Counting has an important role in developing ideas of place value

Challenges for children:

Mastering place value. This may take several years. Coming to terms with confusing irregularities in number words, for example, thirteen could be seen as three and ten, whereas twenty-three reads as two tens and a three. Understanding the part zero has to play in numbers such as 702 or 3 000. In dictation, learning not to write as they hear, for example, not writing 125 as 100205. Recognising the written words for numbers, for example, twelve, fifty. Knowing what “ones” are and that “a ten” means one group of things.

Ways to develop their understanding:

Bundling pegs and threading beads into groups of 10. Building blocks in towers of 10. Matching bundles with numbers. Using spare pages of a graph book for circling amounts, for example, to find 58, circle groups of 10; what is left? Talking about the reasonableness of their answers.

   

PART-WHOLE THINKING

Numbers can be split up into parts and those parts combined into new whole numbers, for example, 8 + 5 = 8 + 2 + 3 = 10 + 3 = 13. There are many ways to make a number, for example, 9 can be made from 7 and 2 or from 6 and 3. Part–whole thinking involves solving problems without the need to count.

Challenges for children:

Taking the risk of moving on from the counting strategy. Learning to see the connections between smaller numbers and larger ones. Children may add 5 and 4 easily but lose their way with 5000 plus 4002 or add 7 + 4 but not see the connection with 17 + 4.

Ways to develop their understanding:

Playing games, such as a Make 10 Snap that forces children to make 10, for example, 6 and then a 4. Helping them make the connection between small numbers and larger ones, for example, 4 + 2 = 6, so 40 + 20 = 60; and 17 + 5 = 22, so 57 + 5 = 62. Helping them to develop a sense and a feel for number through language. Discussion with children about their mathematical activities is essential for their number sense to develop

   

ADDITION & SUBTRACTION

Adding 1 more will give you the next counting number. Order does not matter when adding, for example, (2 + 3) + 4 = 2 + (3 + 4). For every addition fact, there is a related subtraction fact, for example, 6 + 4 = 10, so 10 – 6 = 4. Counting backwards is important for subtraction. Tidy numbers are numbers that end with a zero (10, 100, 50). Compatible numbers add together to give tidy numbers (for example, 41 + 59 = 100). Tidy numbers can also be compatible (for example, for 20 + 20 = 40, knowing smaller numbers such as 2 + 2 = 4 helps make connections to the larger numbers easier). Subtraction is “take away”, but it is also “difference between”.

Challenges for children:

Adding when using zero; Learning that numbers like 51 can be renamed as 4 tens and 11 ones. Understanding place value, for example, that 237 can be expanded to 200 + 30 + 7. When subtracting a larger number from a smaller one, learning not to reverse the numbers, for example, not turning 4 – 6 into 6 – 4

Ways to develop their understanding:

Singing songs or reading simple stories that involve addition or subtraction, for example, “Five little ducks went out one day … only four came home”. Making up number stories using fingers. Threading two colours of beads on a string and adding to find the total, then writing the number story. Playing games that involve addition and subtraction. Encouraging older children to learn the simple things well (for example, addition and subtraction facts to 20) because it helps make the hard maths easy! Writing expressions in a horizontal form (for example, 199 + 99); this forces the children to notice the numbers. (The teaching of vertical form algorithms is left until stage 6.) Helping children with the knowledge they need (for example, 10s and 100s in numbers to 10 000) helps their strategy development

BASIC FACTS (addition and subtraction facts to 9 + 9, multiplication facts to 10x)

There are certain number facts that children need to remember as they meet new ideas in mathematics. For example, 4 x 25 = 100, or 100 centimetres = 1 metre. Basic facts involves knowing about number relationships, for example, knowing that 7 is made up of 5 and 2, or 6 and 1, or 4 and 3. Known facts can be used to find others, for example, using doubling: 2 x 3 = 6, so 4 x 3 = 12.

Challenges for children:

Understanding basic facts learned by rote. Understanding that a fact like 5 x 8 has the same answer as 8 x 5. Not being put off memorising because they think there are too many to learn! Accepting that they still need to be able to instantly recall tables even though they can work them out by using a few known facts,for example, knowing 8 x 5 = 40 or using 8 x 5 is 5 x 5 + 3 x 5 (25 + 15).

Ways to develop their understanding:

Rhythm counting (in time: 1, 2, 3, 4, 5…); stress counting (1, 2, 3, 4, 5, 6); and double counting (3 x 5 so 5, 10, 15 and knowing that 5 is 1 group, 10 is 2 groups, and 15 is 3 groups). Counting in 2s (people's eyes, ears, feet, shoes). Counting in 5s and 10s by relating to hands and feet. As they become more able, making connections between 5x and 10x; 2x, 4x, and 8x; then 3x, 6x, and 9x. Playing games using doubles and squares. Using their hands to help young children know their basic facts to 10 (addition and subtraction). Playing addition and subtraction games, and multiplication and division games.

MULTIPLICATION & DIVISION

Multiplication is about groups of equal size and the number of groups. For example, 3 x 4 could mean 3 groups of 4. Order does not matter when multiplying; the answer is the same, for example, 3 x 8 = 24 and 8 x 3 = 24. When using multiplication, a related division fact can be stated, for example, 5 x 3 = 15 and 15 ÷ 5 = 3. A good knowledge of subtraction and multiplication are needed to work out division problems.

Challenges for children:

Instant recall of multiplication facts. Understanding the remainder in division problems. Language can be confusing. For example, 4 sets of 3 is different to 4 multiplied by 3. Understanding what happens to numbers when they are multiplied by 1 or 0. Attempting division with a poor understanding of subtraction.

Ways to develop their understanding:

Rhythm counting, stress counting, and double counting (see basic facts). Making a set, then having the child copy and then make several equal sets. Giving number stories that they can solve that involve multiplication and division. For example, “Count four buttons into a cup. If each cup is only allowed to have 4 buttons, how many cups would you need if you had 12 buttons?” Setting out equal rows of buttons, covering them, and having the children copy what they have seen. Talking about rows and columns: “Is there a quick way to find out how many buttons there are?” Investigating draws of games, for example, “If there were 6 teams and they all played each other, how many games would be played?”

FRACTIONS

A whole can be divided into equal parts, with the parts called fractions. Each of those parts can be put back together to make a whole. Parts can be joined to make a fraction less than 1. Parts can be joined to make a number more than 1. Fractions can be written in bar notation (1/2) or place value notation (0.5).

Challenges for children:

They may (mistakenly) view a fraction (for example, 7/8) in the same way as they view a whole number. A fraction has two parts to it: the denominator (for example, the 8 in 7/8) is the equal parts that the fraction is divided into; and the numerator (for example, the 7 in 7/8), is the number of like parts. (So 7/8 has 8 equal parts, and we are talking about 7 of them.) Whole number strategies don't work when adding fractions: adding the tops and then the bottoms doesn't give the correct answer. Saying 7 out of 8 reinforces that misunderstanding. What they know about whole numbers doesn't always apply to ordering fractions. There are fractional numbers between whole numbers. There are tenths on the right of the decimal point, not “oneths”.

Ways to develop their understanding:

Finding fractions by cutting paper, fruit, cakes, pizzas; shopping, sharing, cooking. Finding fractions of sets, for example, “What is half of this group of buttons?” Finding halfway along pieces of string. Finding different ways to cut a piece of paper in half or in quarters. Dividing paper into fifths and tenths or quarters and eighths and looking for relationships.

PROBLEM SOLVING

Children become better problem solvers if they have been involved in discussion about the problem. Asking the students what they think the problem is about and encouraging them to act out the problem or draw diagrams helps them to build up problem-solving strategies. As the students become more able, help them develop a problem-solving plan, such as the four-step one below: Read and understand the problem. What is the question asking? Make a plan. Where will you start? What are your ideas? Carry out the plan. Are you able to work the problem out? If not, start again. Look back. Have you answered the question? Make changes if necessary.

Possible challenges for children in all areas:

Being able to quickly access and use the mathematical vocabulary needed. Being able to read, with understanding, what the problem is asking. Being able to communicate clearly the processes and/or strategies they are using.